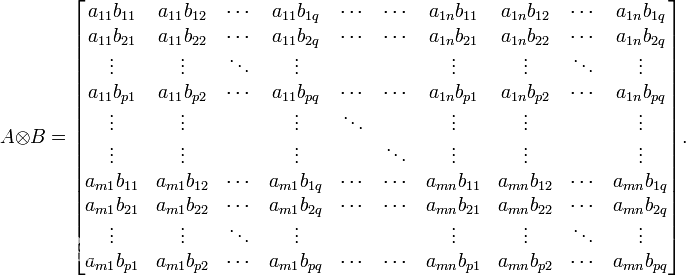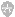对n×m阶矩阵A和p×q阶矩阵B,A和B的Kronecher乘法运算可定义为:
Module KroneckerProduct_Mod
Implicit None
Integer , parameter , private :: DP = Selected_Real_Kind( 9 )
contains
Subroutine KroneckerProduct( A , B , H )
Real( Kind = DP ) , Intent( IN ) :: A(:,:) , B(:,:)
Real( Kind = DP ) , Intent( OUT ) :: H(:,:)
Integer :: i , j , m , n , p , q
m = size( A , dim = 1 )
n = size( A , dim = 2 )
p = size( B , dim = 1 )
q = size( B , dim = 2 )
Do i = 1 , m
Do j = 1 , n
H( p*(i-1)+1 : p*i , q*(j-1)+1 : q*j ) = B * A(i,j)
End Do
End Do
End Subroutine KroneckerProduct
End Module KroneckerProduct_Mod
Program www_fcode_cn
use KroneckerProduct_Mod
Implicit None
Integer , parameter :: DP = Selected_Real_Kind( 9 )
Integer , parameter :: m=2 , n=3 , p=4, q=5 , index1 = m*p , index2 = n*q
Real(kind=DP) :: A(m,n) , B(p,q) , H(index1,index2)
integer :: i
A = reshape( (/1,2,3,4,5,6/) , (/2,3/) )
B = reshape( (/1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20/) , (/4,5/) )
call KroneckerProduct( A , B , H )
Do i = 1 , index2
Write(*,'(8(f5.1,1x))') H( :, i)
End do
End Program www_fcode_cn