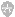关于截断误差和舍入误差的简单示例
2015-08-21 15:46:11   来源：jason@fcode   评论：0 点击：

采用浮点数计算时，因为计算机字长有限，通常无论采用什么样的算法均会存在一定的截断误差和舍入误差。
因此，在编程时对这两种误差有比较清醒的认识显得尤为必要。
Steven C. Chapra在”Numerical Methods for Engineers“一书中采用泰勒公式对此进行了分析，并给出了Matlab示例。

本人把这个例子转化为了下面的Fortran代码，供大家参考。
因为Fortran无法直接绘图，计算结果的图示是通过Gnuplot实现的。

该例子采用中心差分计算在x=0.5时函数f(x)=−0.1x^4−0.15x^3−0.5x^2-0.25x+1.2的一阶导数随步长的变化，其具体说明参见原书，在此不再赘述。

program www_fcode_cn
  implicit none
  integer :: i
  real(8) :: h,d,e,x,dftrue
  open(10,file='result')
  write(10,'(a)')'# step size  finite difference   true error'
  x=0.5_8
  dftrue=dfunc(x)
  h=1
  do i=1,11
     d=(func(x+h)-func(x-h))/(2*h)
     e=abs(dftrue-d)
     write(10,'(f12.10,x,f17.14,x,f15.13)')h,d,e
     h=h/10
  end do
  close(10)
contains
  function func(x)
    real(8) :: x,func
    func=-0.1_8*x**4-0.15_8*x**3-0.5_8*x**2-0.25_8*x+1.2_8
  end function func
  function dfunc(x)
    real(8) :: x,dfunc
    dfunc=-0.4_8*x**3-0.45_8*x**2-x-0.25_8
  end function dfunc
end program www_fcode_cn

计算结果文件result的内容为：
# step size         finite difference      true error
1.0000000000 -1.26250000000000 0.3500000000000
0.1000000000 -0.91600000000000 0.0035000000000
0.0100000000 -0.91253500000000 0.0000350000000
0.0010000000 -0.91250034999996 0.0000003500000
0.0001000000 -0.91250000349985 0.0000000034998
0.0000100000 -0.91250000003318 0.0000000000332
0.0000010000 -0.91250000000542 0.0000000000054
0.0000001000 -0.91249999945031 0.0000000005497
0.0000000100 -0.91250000333609 0.0000000033361
0.0000000010 -0.91250001998944 0.0000000199894
0.0000000001 -0.91250007550059 0.0000000755006




从计算结果可以看出，当步长减小时，截断误差在减小，但当步长减小到一定程度后，舍入误差在增大。

因此，在实际计算时并非步长越小越好。在这个例子中，当步长在百万分之一左右时总体误差最小。